For example, if rating is a list of ratings across items,
rating > 3 returns a list of boolean values, with true for ratings over 3 and false for those equal to or lower than 3.
This result can then be fed to a count() function, so that a nicely readable count(rating > 3)
returns the number of items with a rating over 3.
Chapter 4
Formula²: A Human-centric Hierarchical Formula Language
Contents
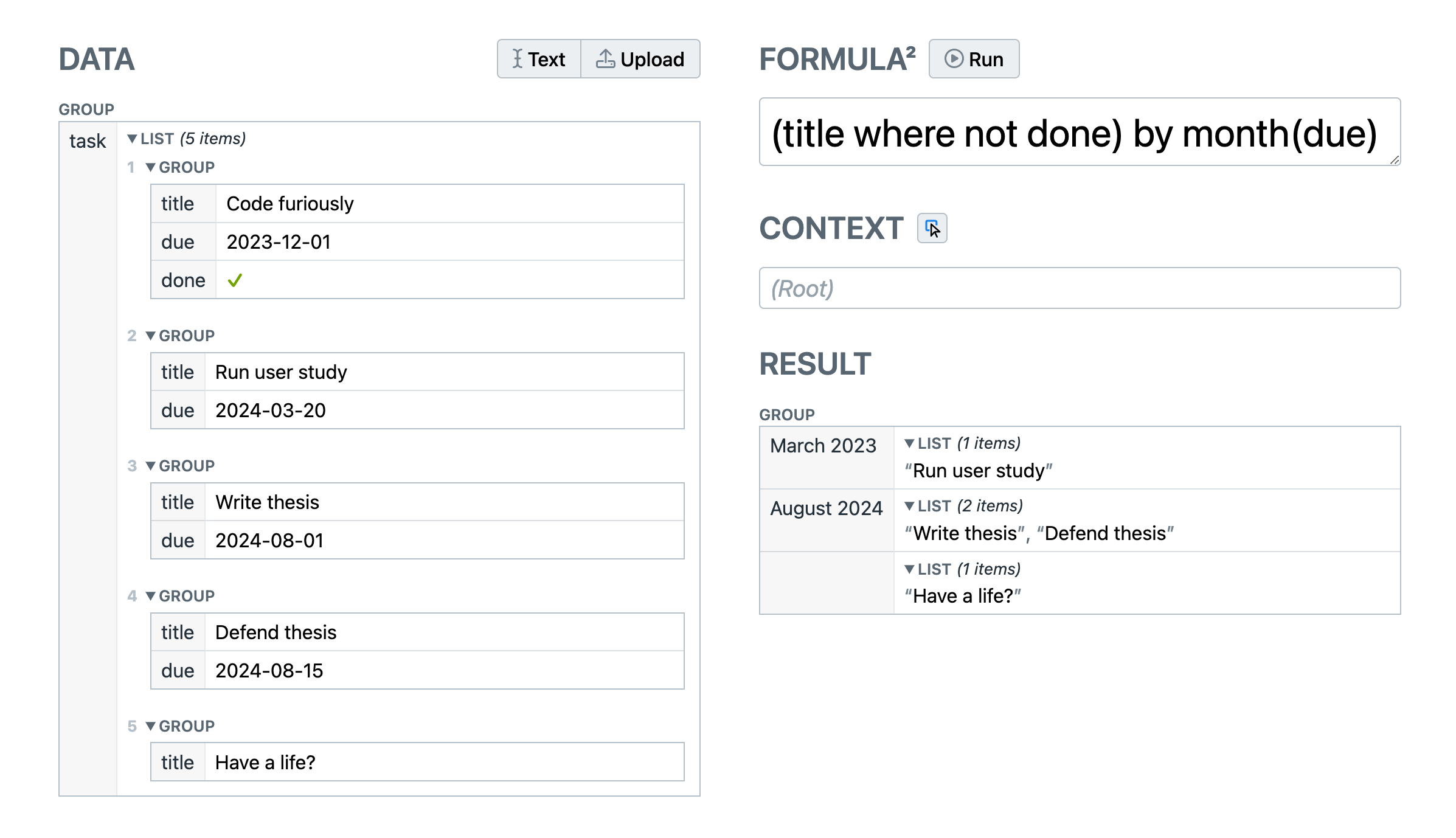
A Formula2 formula operating on a shallow hierarchical schema,
showcasing implicit scoping (title, done, due),
filtering & grouping operators, and temporal computation.
Parentheses around the where expression are added for clarity
— operator precedence rules would produce the same result.
4.1Introduction
Spreadsheets introduced reactive (aka continuous evaluation [1]), side-effect free formulas to the massses, and despite the well-known limitations of spreadsheets [2], no other end-user programming environment has managed to surpass their popularity.
Despite hierarchical data naturally occurring in more than half of data structures novices organically create [3], few formula languages support hierarchical data structures. Moreover, the few that do often prioritize compatibility with spreadsheets over natural programming and general HCI principles.
Formula² (MavoScript in earlier literature [4]) is a formula language designed from scratch to support hierarchical data structures in a way that is natural for novices and reduces the amount of abstract thinking about data required.
However, if the research question was simply How can we design a natural formula language?
,
the answer is simple — no structured language can beat natural language at that — almost by definition.
But parsing natural language is resource-intensive and error-prone,
so instead we designed Formula2 to answer the question
What would a formula language look like if it were designed from scratch today,
with the explicit goals of prioritizing usability, natural programming principles [5, 6],
and making common use cases easy,
while still maintaining reasonable parsing and evaluation complexity?
Indeed, while our user studies repeatedly demonstrated that Formula² was easier for novices than alternatives, it can be parsed very efficiently with a simple Pratt parser [7].
While Formula² was originally developed for Mavo, it has no dependency on any particular host language or system. It could be used on hierarchical spreadsheet-like applications, compiled to JavaScript and used by JavaScript frameworks, or even used in a standalone environment against arbitrary data (see Figure 4.1). Consistency with JavaScript or other web technologies was not a primary design consideration for its syntax, but was used as a tie-breaker for otherwise equally valid design decisions.
4.2Related Work
Since LANPAR introduced reactive formulas in 1969, and VisiCalc augmented them them in 1979 with the A1 notation and most of the features we know today [2], a lot of work has been done to improve on their design.
4.2.1Hierarchical Data in Spreadsheets
Gneiss [8, 9] was a spreadsheet system supporting hierarchical data. However, the bulk of its contributions were in the user interface. Its formula language prioritized compatibility with spreadsheets and thus, included the minimum amount of changes needed to support hierarchical data. References to data still used the obscure A1 notation, just extended it for nested data.
4.2.2Reactive Formulas Operating on Databases
SIEUFERD [10] provided a spreadsheet-like hiearchical data interface to a SQL database, and thus had to design a formula language that could handle hierarchical data. While it used readable names rather than A1 notation, compatibility with spreadsheets was a primary design goal. More importantly, the primary means of querying list-valued data was its interface for visually constructing SQL queries, and thus the formula language is purposefully restricted to scalars as a return value.
4.2.3Reactive JavaScript Frameworks
Spreadsheet formulas are not the only syntax in wide use for reactive formulas. While spreadsheet formulas are the most popular end-user programming syntax for reactive formulas, this section would not be complete without mentioning the many reactive JavaScript frameworks, such as VueJS [11], Angular [12], or Svelte [13] These frameworks typically support embedding a restricted subset of JavaScript in HTML, and detect dependencies by parsing the JavaScript code.
4.2.4Other Dataflow Languages
There are many other dataflow languages, such as LabView [14], a visual programming language for dataflow programming. However, these are typically not designed for end-users, and are often not reactive in the same sense as spreadsheet formulas. The usability issues with LabView are well-documented [15].
Mashroom [16] was a dataflow language designed for mashups, and operating on nested tables. While some of its operators were similar to Formula², and it also centered around aggregation, it required a lot more technical knowledge to use and targeted different use cases.
4.3Syntax and Core Concepts
In this section we summarize Formula2’s core concepts and syntax. A more detailed design discussion can be found in Section 4.5.
4.3.1Separation of Concerns
We define the host environment as the environment in which Formula² is embedded. This could be a spreadsheet-like application, a no-code visual app builder, a web framework, or a standalone application that allows the user to directly import data, specify Formula² expressions, optionally select the context node (see Section 4.4.1), and see the result (Figure 4.1). We have already seen one host environment, Mavo HTML.
Since Mavo is the only host environment of Formula² that we have seen so far, it may be unclear where Formula² ends and the host environment begins. Formula² is responsible for (a) parsing and compling expressions, and (b) evaluating them against an arbitrary data tree. To maximize flexibility and make it easier to adopt by a variety of host environments, monitoring dependencies and re-evaluating expressions at the appropriate times is handled by the host environment.
It could be argued that this makes Formula2 simply a functional, side-effect free language, since it is the host environment that may (or may not) implement it reactively. For example, the testing host environment shown in Figure 4.1 does not implement any reactivity. However, we believe this to be an implementation detail. The language design and semantics assume a reactive implementation. The fact that it can function (and even be useful) without reactivity is a testament to its flexibility.
4.3.2Syntax and Semantics
An explicit design goal was to minimize the number of syntactic primitives that need to be learned, and instead allow as many combinations of these primitives as possible.
- Literals: Numbers, strings (enclosed in single quotes, double quotes, or none (see below)), booleans (
true/false), empty values (none) - Identifiers: Any string of letters, numbers, or underscores.
$is also allowed, but is reserved for predefined Formula2 identifiers. - Function calls are invoked with the usual syntax of
functionName(arg1, arg2, ...). Commas are optional, but encouraged. - Operators, which can be unary, binary, ternary, or n-ary.
Complex data types such as lists and groups are also constructed using functions and operators.
4.4Core Contributions
In this section, we present the core concepts that position Formula² in the landscape of reactive formula languages.
4.4.1Implicit Scoping and Aggregation
Consider the use case shown in Figure 4.1. If we were using JavaScript, the expression could look like this:
tasks.reduce((acc, task) => {
(acc[month(task.due)] ??= []).push(task.title);
}, {})
Going beyond syntactic differences, referencing in JavaScript (and most other programming languages) is shallow: we cannot reference any task properties without getting ahold of each task object, and we could do that without iterating over the list of tasks. There are two levels of indirection to go from the data root to the data we are interested in. This approach minimizes conflicts, but at the cost of verbosity and complexity.
In natural language, scoping is a way to optionally narrow, not a prerequisite for meaning. Any known object can be referenced, and the context of the conversation is implicitly used to resolve it. This process may even involve iteration or even a recursive walk through the hierarchy of known objects, yet humans handle it effortlessly.
We can say put all dirty dishes in the dishwasher
without needing to specify
whether the dishes are on the table, in the sink, or in the bedroom.
We can optionally scope it further, e.g. put all dirty dishes from the dinner table in the dishwasher
,
but the scope is optional, and the dirty dishes concept has meaning without it, just broader.
In contrast, while programming languages also have a notion of context, references are typically more restricted. Context typically simplifies references to identifiers directly within the current scope, or in ancestor scopes, but that’s about it. Getting descendant or sibling data typically requires a series of recursive mapping operations. To word the dirty dishes example using the concepts of most programming languages, we would have needed to say something like:
“Visit every room in the house and do the following. If there are any dirty dishes on the floor, put them in the dishwasher. Look for objects with horizontal surfaces, then look for dirty dishes on them. If you find any, put them in the dishwasher. Now look inside all containers larger than a plate. If you find any dirty dishes, put them in the dishwasher. If you find other large enough containers, repeat the process for them too.”
Imagine how tedious communication would be if we had to speak like this! And yet, we have accepted that this is a reasonable way to communicate with computers.
This could explain why scoping and referencing errors are so common among beginner programmers [17–19]. The need to understand scoping rules, write out lengthy namespaces, or — worse — mapping operations when multiple values are desired are all barriers to entry. To alleviate this, Formula² uses a novel scoping algorithm that will prioritize explicit references over implicit ones, but will attempt to resolve any known identifier to the most reasonable author intent, taking into account both the structure of the formula, the data schema, as well as the placement of the formula relative to the data.
In Formula², any known data identifier can be used anywhere. However, the value(s) it resolves to depends on the placement of the formula. Every evaluation of a Formula² expression can be associated with a context node in the data.
This is in contrast with scoping in most programming languages, which is either lexical (derived from the code hierarchy) or dynamic (derived from the call tree). Typically the context node would have a spatial association with the formula in the host environment, for example in Mavo it would be the closest containing property. In a spreadsheet it could be the cell the formula is in.
A given identifier can resolve to a single value or a list of values, depending on the relative locations of the context node, the data it references, and the data schema.
Conceptually, to resolve the value of an identifier, we perform a breadth-first search1This is a simplification and would result in very poor performance. In practice, the Breadth-First Search is performed on a precomputed schema of the data, and then the paths are resolved on the actual data. on the data to find the shortest path(s) from the context node to properties with the given identifier. We then resolve these paths to values. If there are more than one paths, or the paths cross any arrays (even if they only contain one element), the result is a list of values.
If the property is not found at all, then ancestor nodes are searched for the property.
While this algorithm may sound complex, in practice it affords a more natural way to reference data, where references largely just work and scoping rarely needs to be explicitly considered.
4.4.2Transparent List-valued Operations
Since lists are such common return types,
built-in support for list operations is essential.
But Formula² goes a step beyond that, and attempts to blur the line between scalar and list operations.
Its answer to “Am I dealing with a list or a scalar?” is if you don’t already know, it shouldn’t matter
,
in the sense that the author providing a list or a scalar communicates intent,
and that intent is generally honored,
but whether a function’s return value is a list or a scalar should largely be irrelevant,
except when it’s a predictable consequence of said author intent.
Part of this is a natural consequence of the scoping algorithm.
Since foo.bar looks at descendant properties via a breadth-first search,
the result will be the same whether foo is a single object with the foo property
or a list containing said object as its only element
(since Formula² lists don’t include arbitrary data properties).
Nearly all Formula² operations (functions and operators) are list-aware. Operations on lists, between lists, or between scalars and lists require no special syntax or functions. They largely just work.
The algorithm used is simple. Operations (including functions) are defined in terms of their scalar equivalents.
- When both operands are scalars, the scalar operation is applied.
- When only one operand is scalar, the result is a list where each list item is the result of applying the operation to the scalar and the list item.
- When both operands are lists, the operation is applied element-wise.
If the lists have different lengths,
nullis used for missing values.
Lists returned from operations are flattened,
so that all data is either scalars or lists of scalars,
i.e. authors do not need to deal with lists of lists.
This was chosen to limit complexity,
as lists of lists are less common in naturally occurring data structures [3],
and create amgibuities for many operations
(e.g. what should count(list) return if list is a list of lists?
The number of lists or the total number of elements?).
4.5Detailed Design Discussion
We now present the design of Formula², focusing on its syntax and semantics.
4.5.1Fault-tolerance & Flexibility
The design principle of fault tolerance (Section 1.4.4), permeates many of the design decisions of Formula²:
- Case-insensitivity: Function names and identifiers are case-insensitive, so
rating,Rating, andRATINGwill resolve to the same result. - Graceful references: Using the narrowing (
.) operator on an empty value, does not produce an error, just a result that is also an empty value. - Unquoted strings: Unquoted strings are allowed, but are a last resort if an identifier cannot be resolved as data.
4.5.2Special Properties
Most formulas depend on the values of other data, and should update when those values change. However, some use cases require access to context data that may change even if no data has changed, and thus should influence when a formula is recalculated, essentially adding itself to its dependencies.
For example, a formula that displays the current time in hours and minutes should update at least every minute,
even if no data has changed.
In spreadsheets, this is expressed as a function, NOW().
However, function calls do not update dependencies, so NOW() has the confusing behavior that it does not actually reflect current time now
,
but the time the row was last edited (which is a useful piece of information in its own right,
but needs a name that better describes its purpose).
In Formula², such computations are expressed as special, built-in properties
beginning with $.
For example, the current time is expressed as $now.
Other examples of special properties are:
$mouse, which provides the current mouse position and updates whenever the mouse moves.$hash, which returns the current URL hash (without the#sign) and updates when the hash changes.$today, which returns the current date and updates at midnight.
There are also several tree-structural special properties,
which are used to navigate the data tree.
For example, $parent to reference the parent of the current context node,
$previous and $next to reference its siblings,
$all to go from an item to its containing list,
or $index to get the index of the closest list item
(or any list item, when used as a property)
While the $ prefix is designed to prevent clashes with author identifiers
by partitioning the namespace,
we noticed in user studies (see Chapter 7) that authors often forget to use it,
presumably because this is an unnatural use for the $ symbol,
which in natural language is used for currency.
It remains an open problem how to partition the namespace in a way that is more intuitive to authors,
without making it overly verbose (as in the case of a reserved prefix, e.g. f2_now).
In line with its design principle of fault tolerance (Section 1.4.4),
Formula² will attempt to resolve special property identifiers without the $ prefix,
but with a lower priority than those with the $ prefix,
only if no data properties exist with these names.
It will also correctly resolve author identifiers that begin with $.
4.5.3Data Types
Formula² supports the following data types:
- Numbers
- Strings, enclosed in single or double quotes. Unquoted strings are also supported if they only consist of identifier-compatible characters, but have lower precedence than data references. Since the schema can be mutated at runtime, this means their meaning could change if a new property is added anywhere in the data that matches the unquoted string.
- Booleans,
trueandfalse. - Empty values (aka
null) - Lists (aka arrays or collections).
Lists can contain any data type.
There is no dedicated syntactic construct for lists, instead they are defined via a
list()function. - Groups (aka objects or dictionaries), which are sequences of key-value pairs.
Groups are defined using a
group()function and a colon to separate keys from values.
{
"name": "Lea",
"age": "32",
"hobby": [
"Coding",
"Design",
"Cooking"
]
}
group(
name: Lea,
age: 32,
hobby: list(
Coding,
Design,
Cooking
)
)
A JSON object and the corresponding representation in Formula².
The colon (:) is actually an operator that returns an object with a single key-value pair.
The group function merely merges these objects.
This has the very nice consequence that when there is only a single key-value pair,
the group() function can be omitted.
4.5.4Operators
Operators are essentially a nicer syntax to improve readability for certain functions, and to reduce the need for balancing nested parentheses. All operators are also implemented as functions (but the contrary is not true).
To improve learnability, only widely understood operators are symbols:
- common arithmetic operators:
+,-,*,/ - common comparison operators:
>,<,>=,<=,=(and==),!=, - concatenation:
&, - the key-value pair operator:
: - the range operator:
..
All other operators are words,
including
logical operators (and, or, not),
a modulo operator (mod),
filtering (where),
grouping (by / as).
These are designed to eliminate many common types of errors across novice programming and formula languages [20, 21]:
- To avoid confusion between
=and==,=and==are both used for comparison. - It is common for
+to do double duty: addition or concatenation, heuristically determined by the operands. This usually leads to errors, when the heuristics predict author intent incorrectly. Moreover, such a heuristic does not improve ergonomics since addition and concatenation are fundamentally distinct operations. In Formula²,+is only used for addition, and&is used instead for concatenation. This allows+to work even when numbers are stored as strings, sparing novices from having to think about data types. - Unlike most programming or formula languages, comparison operators are n-ary.
For example,
3 < foo < 5is perfectly legal and equivalent to(3 < foo) and (foo < 5).
4.5.5Operators That Affect Scoping
In certain cases, Formula²’s innovation of implicit aggregation becomes its Achilles’ heel. A big class of these are operations whose operands are not independent, but one operand is implicitly scoped by the other.
4.5.5.1Narrowing Operator (.)
The most trivial such case is the narrowing (or dot) operator, which is used to access properties of objects and to narrow down overly broad references.
With most operators, operands are resolved independently.
For example, in the schema shown in Figure 4.1, a formula like title & " " & due would evaluate title to all task titles, due to all task due dates, and would then concatenate them element-wise separated by a space.
However, if the same approach were followed with the dot operator,
it would produce nonsensical results.
Imagine if given a reference like students.name we evaluated students and name separately!
Instead, students essentially adds a constraint to the resolution of name:
it says “only consider name properties that are descendants of students”.
Whether this constraint is implemented by fetching all students objects and then looking within them, or by resolving name independently and then filtering it, is left up to implementations.
4.5.5.2Filtering and Grouping Operators (where and by)
A less obvious example is the filtering operator (where).
To enable filtering of list-valued properties, Formula² supports a where operator and a corresponding filter() function.
The filter() function takes two lists
and returns a new list that contains only the elements of the first list for which the corresponding element in the second list is not empty, false, or 0.
Any surplus elements in the second list are ignored per existing list operation semantics (Section 4.4.2).
However, a where b is not simply syntactic sugar for filter(a, b).
There is one common ambiguity that where resolves:
should properties referenced in predicates be resolved by the context node of the expression as a whole, or in a different way?
This is best explained with an example.
Consider the schema in Section 4.7.2.
Assuming a decision item context node, what would you expect the expression pro where weight > 2 to return?
Presumably, you would strongly suspect it should return pro objects that have a weight property over 2.
However, if where were naïvely rewritten, it would be equivalent to filter(pro, weight > 2).
Like every function, each argument is resolved separately:
pro resolves to all pros of the context decision,
and weight > 2 resolves to a list of booleans …for all weights — including weights for cons!
To get the expected result with the filter() function,
we need to use the narrowing (dot) operator and write filter(pro, pro.weight > 2).
To prevent this terribly confusing behavior,
where is implemented to apply special scoping rules,
to preferentially resolve properties in the second operand
as descendants of the first operand.
This is not the same as naïvely prepending identifiers with a narrowing operator involving the first operand,
nor as using the first operand as a context node:
When we write foo.bar, if bar is not found within foo and its descendants,
the return value is empty2The implementation of Formula² that the Mavo HTML prototype embeds does not actually follow this; a bug that has caused a lot of confusion..
However, in the case of foo where bar > N, if bar is not found within foo and its descendants, we do want the search to continue as normal within the context node of the formula.
It could be argued that using foo as a context node and continuing the search to its ancestors is also reasonable, but in practice that is rarely desirable and has similar issues as dynamic scoping.
The closest rewriting would be (foo.bar or bar)
4.5.5.3Explicit Scoping Operator (in)
In some cases, it makes sense to evaluate an identifier using a different context node than the one of the whole formula. One area where this is needed is nested aggregates, i.e. aggregates of aggregates. We use nested aggregates when in a hierarchical schema we want to compute an aggregate within descendant lists and then aggregate the aggregates at a higher level of the tree.
This may sound obscure in the abstract, but use cases that require nested aggregates are quite common in data-driven applications.
For example, assuming the data schema of a restaurant review website, average number of reviews
is a nested aggregate: AVERAGE of COUNT.
To support this, Formula² supports an explicit scoping operator, in,
which evaluates its first operand in the context of the second operand.
The in operator has slightly different semantics around list values than other operators (Section 4.4.2):
if the second operand (the scope) is a list, the first operand is evaluated for each item in the list.
This is because it actually affects what the first operand resolves to,
so taking its shape into account would create a logical cycle.
The scoping operator facilitates nested aggregates using a concise, natural syntax.
Returning to the restaurant review example,
to calculate the average number of reviews per restaurant,
we would write average(count(reviews) in restaurants).
It can also facilitate complex object mapping operations, though the syntax can be a little more awkward.
For example, assume we have a list of right triangles (triangle) as objects with width and height properties.
We can easily calculate a list of hypotenuses with sqrt(pow(width, 2) + pow(height, 2)),
but what if we want to transform it to a list of triangles with width, height, and hypoteneuse properties?
This would work, but a novice would be unlikely to write it:
group(triangle, hypotenuse: sqrt(pow(width, 2) + pow(height, 2))) in triangle
Due to the potential for confusion, its precedence is very high so that authors are forced to use parentheses to scope expressions with more than one term.
4.5.6Escaping the Scoping Heuristic
In many common cases, Formula²’s scoping heuristic can save authors time and effort. However, as with many heuristics, there are cases where the heuristic would incorrectly predict author intent. Per our design principles (Section 1.4.3), inferred author intent should be overridable.
For such cases, Formula² provides several ways to disambiguate references, either by using more narrow scoping, or by providing ways to tweak reference resolution:
- If ancestor values are undesirable, a narrowing operator (
.) can be used to scope references to be within a specific object. - Special properties such as
$parent,$previous,$next,$item,$thiscan be used to navigate the data tree of a given reference. - If the entire list of values is desired from a formula within a list, the
$allspecial property can be used.
For example, in a list of restaurants, if the formula rating was on or within each restaurant,
it would resolve to a scalar value: the rating of that restaurant.
However, if rating is used outside the list of restaurants,
it would resolve to a list of ratings of all restaurants.
So what if we want to show where the current restaurant stands compared to all others in the list?
100 * count(rating.all > rating) / count(rating.all)
would give us the percentage of restaurants with a higher rating than the current one,
which would allow us to output things like “Top 5%”.
4.5.7Easier Temporal Computation
We identified temporal math as a common pain point when working with spreadsheets and later validated that our hypothesis was true (see Section 7.6). Yet, temporal computation is ubiquitous in so many types of web applications, from use cases like personal tracking and project management to simple things like showing the date a post was created, or how long has passed since.
Formula² provides a variety of functions to support manipulating and formatting temporal values across various points of the ease-of-use to power spectrum.
Dates, times, and date/times are represented as ISO 8601 [22] strings. If a mathematical operator is used with at least one string operand (which cannot be parsed as a number), Fomula² will check if the string is a temporal value, and will perform a temporal calculation if so.
This allows authors to specify temporal values by simply specifying them as strings,
with no additional effort to convert them to a specific data type.
Since no valid ISO dates are also valid numbers3The only exception is years, since something like "1997" is actually a valid ISO date.
However, this does not participate in the heuristic discussed here,
since if authors are doing math between years, there is nothing special to do — handling them as regular numbers works fine., this is a safe heuristic.
A variety of built-in functions and special properties are provided to make such operations natural to read and write.
For example date($today + 1 * day()) will return tomorrow’s date
and duration($now - "2019-07-12", 2) will return how long it has been since July 12th, 2019
in a human-readable format with two terms (e.g. “3 years, 2 months”).
Temporal expressions involving special properties such as $now should be updated by the host environment at a reasonable rate,
up to display’s framerate, to ensure that they are always up-to-date.
While Formula² does not specify optimizations for this (e.g there is no need to update readable_date($now) at 60 fps),
host environments are encouraged to do so.
The ISO 8601 format also supports timezones, and these are honored in any calculations. However, it remains important future work to provide more primitives for their handling. If no timezone is specified, the user’s local timezone is assumed.
4.5.8Internationalization & Localization
Any functions that produce human readable output (such as many temporal functions) are locale-aware:
the host environment can optionally associate a locale with certain data nodes (any node without a locale inherits the locale of its parent),
and output follows this locale.
For example, in Mavo, the locale is derived from the closest HTML lang attrbute.
4.6Architecture
Here we summarize some architectural considerations for implementing Formula².
4.6.1Expression Compilation
4.6.1.1Grammar
Ease and efficiency of parsing was a key design consideration. The entirety of Formula2’s syntax can be parsed by a simple Pratt parser [7]. In fact, all that is needed to adapt a Pratt parser intended for JavaScript expressions4JSEP: ericsmekens.github.io/jsep to a Formula² parser is to simply modify its operators.
| Operator | Description | Precedence | Associativity |
|---|---|---|---|
() |
Function call, grouping | 15 | Left |
. |
Narrowing operator | 14 | Left |
not, -, + |
Unary operators | 13 | Right |
*, /, mod |
Multiplication, division, modulus | 12 | Left |
+, - |
Addition, subtraction | 11 | Left |
<, <=, >, >= |
Comparison operators | 10 | Left |
=, ==, != |
Equality operators (equal, not equal) | 9 | Left |
and |
Logical AND | 8 | Left |
or |
Logical OR | 7 | Left |
where |
Filtering operator | 4 | Right |
by / by ... as |
Grouping operator | 3 | Right |
in |
Explicit Scoping operator | 2 | Left |
, |
Separator in function arguments, etc. | 1 | Left |
Precedence and associativity of Formula² operators.
To generate a Pratt parser for Formula², the operator associativities and precedences are shown in Table 4.1. On a high level5The productions do not enforce operator precedence, which is specified seprately, and do not describe the minutiae of number and string literals, which are on par with JavaScript or similar languages., an EBNF grammar for Formula² could look like this:
Expression: Operand | Compound
Operand: Literal | Identifier | UnaryExpression
| BinaryExpression | MemberExpression | TernaryExpression
| CallExpression | '(' Expression ')'
UnaryOperator: 'not' | '-' | '+'
UnaryExpression: UnaryOperator Operand
BinaryOperator: ['<' | '>' | '='] '='? | '!=' | '*' | '/' | '+' | '-'
| 'mod' | 'and' | 'or' | 'where'
MemberExpression: [ [MemberExpression | Identifier] '.' ]+ Identifier
BinaryExpression: Operand BinaryOperator Operand
TernaryExpression: Operand 'by' Operand [ 'as' Operand ]?
CallExpression: [ Identifier | MemberExpression ] '(' Compound ? ')'
Compound: Expression [ Separator [ Expression | Compound ] ]+
Separator: ',' | ';' | whitespace
| any other non-alphabetic, non-numeric character
Literal: Numeric literals (e.g., 1, -42, 3.14)
| Single or double-quoted string literals
Identifier: ['$' | letter | '_'] [ letter | digit | '_' | '$' ]*
4.6.1.2AST Transforms and Desugaring
After parsing, a number of AST transforms are applied to the parsed expression. These include:
- Flattening logical operators. For example,
3 < foo < 5will be parsed as(3 < foo) < 5, which would produce an incorrect result. Only logical operators need to be flattened. Other operators are either correctly handled via normal precedence rules, or are associative and thus flattening would make no difference. - Rewriting operators into their equivalent functions (with further rewriting for operators that affect scoping, see Section 4.5.5).
- If the left operand of
:is an identifier, it is rewritten to a string literal.
4.6.2Expression Evaluation
4.6.2.1Building a Schema
While Formula2 is not dependent on any particular language or system, to avoid excessive abstraction, we will describe its implementation in terms of JavaScript concepts.
For Formula² to be able to evaluate expressions against a data tree, it first needs to walk the data tree to understand its structure and to store pointers from data objects to this stored information.
This involves:
- Walking the data tree to build a schema (unless this is precomputed by the host environment). This is not a detailed data schema; for example it does not concern itself with data types at all. It is simply a nested data structure of all possible property paths to help resolve identifiers.
- Linking each node to its parent, so that traversal in any direction is possible from any node.
- Linking each object to its corresponding schema node, so that traversal in any direction is possible.
Building a schema is not merely a performance improvement: it is essential for reasonable identifier resolution. Imagine if the meaning of identifiers changed simply because a collection happened to have no items at the moment of evaluation! Of course it is also a performance improvement — performing a breadth first search on the data tree for every identifier would be prohibitively slow even for modestly sized datasets.
The host environment needs to notify Formula² when the data tree changes in a way that affects the schema so it can be rebuilt, otherwise expression evaluation could be incorrect.
{
task: [
{
taskTitle: "Code furiously",
done: true,
tags: ["coding", "fun"],
},
{
taskTitle: "Run user study",
priority: "P2",
tags: "science"
},
"Have a life?"
]
}
{
task: [
{
taskTitle: true,
done: true,
priority: true,
tags: [true]
}
]
}
A data tree on the left and its generated schema on the right. List items are merged into a single schema node, and arrays win out over scalars.
4.7Comparison with Other Languages
We now present a few examples that highlight how Formula² provides improved ergonomics over JS, spreadsheet formula languages, and SQL. Each example schema has been chosen as a representative example of a common data shape. First, a flat table. Then, a schema with divergent one-to-many relationships with the same schema. Finally, a schema with a deeper hierarchical structure.
For the comparison with JS, we will use the scoping convention of many JavaScript frameworks, that identifiers directly below the context node can be referenced directly, as well as ancestor properties, but everything else requires explicit scoping.
To compare with spreadsheets and SQL, there is a dilemma: how to best convert a hierarchical schema to a tabular one to maximize the comparison fairness?
There are three main ways:
- Denormalization: Flatten the data structure into a single table with repeating values, akin to the result of a SQL join.
- Normalization: Split the data structure into multiple tables, with foreign keys linking them. 2NF ([23]) is probably sufficient for this.
- Blank cells: Use blank cells where (1) would repeat values.
The latter is what is most readable to humans and what they often naturally gravitate to, as it does not require duplication (1), yet does not involve the complexity and indirection of relations (2). Effectively it is trying to visually emulate a hierarchy, and it works — for (sighted) humans. However, it is actively discouraged [24] as it breaks any type of data processing (e.g. formulas, filtering, sorting, etc.).
Repetition is a common way, albeit tedious to manage manually. However, repetition becomes very awkward when we have divergent one-to-many relationships [10], as is the case in one of the schemas below. This only leaves us one option: normalization.
In many cases, defining additional data in the host UI (e.g. computed properties in Mavo, or additional columns in a spreadsheet) would make some of these expressions a lot simpler, but to ensure a fair comparison, we will only use the data as it is defined in the schema. Additionally, we know from Section 7.6 that it is a barrier for novices when a computation requires auxiliary data to be defined in the UI.
For tasks that involve a context node, it is mentioned. Otherwise, the context node is assumed to be the root of the data tree.
4.7.1Flat Table: The To-Do List Schema
This is a variation of the to-do app shown in Section 1.2.
{
task: [
{
taskTitle: "Code furiously",
done: true,
priority: "P2",
due: "2022-07-12T12:00:00Z",
}
]
}
| taskTitle | done | priority | due |
|---|---|---|---|
| Code furiously | true | P2 | 2022-07-12T12:00:00Z |
4.7.1.1Simple Aggregates: Percentage of Tasks Done
This is a simple aggregation task, so it mainly highlights syntactic differences across the four languages.
count(done) / count(task)
COUNTIF(B2:B, true) / COUNTA(B2:B)
task.filter(t => t.done).length / task.length
SELECT count(done) / count(*) FROM task
4.7.1.2Grouped Aggregate: Count Tasks by Priority
Here we want a data structure that will give us priorities and the number of tasks with that priority.
Aggregate functions like count() have a special behavior with the results of grouping,
and return a list with the counts of all groups.
We can get the group names either as (task by priority).tasktitle
or simply unique(taskTitle), since it is guaranteed to produce the same results, in the same order.
The colon operator can help us combine the two into a single object:
unique(taskTitle): count(task by priority)
This is not possible to do in spreadsheets as the result of a single formula.
Spreadsheets have a dedicated UI feature for this called pivot tables, although no-one tried to use them in our study (Section 9.7).
The closest we can get with the regular primitives is to
add a column E to the table, place the formula =COUNTIF(C2:C, C2) in E2, and drag it down.
Since UI interactions are not acceptable in this comparison, we will not consider this option. We could get an arrayformula with a list of strings like “P0: 2”, “P1: 3”, etc. like this:
=TEXTJOIN(", ", TRUE, ARRAYFORMULA(UNIQUE(C2:C7) & ": " & COUNTIF(C2:C7, UNIQUE(C2:C7))))
In JS, it could look like this:
task.map(t => t.priority).reduce((acc, p) => {
acc[p] = (acc[p] || 0) + 1;
return acc;
}, {})
Contrary to the other two, these tasks are SQL’s bread and butter:
SELECT priority, count(*) FROM task GROUP BY priority
4.7.1.3Temporal: Display Time Left for Each Task
This is a simple temporal computation task. More than showcasing the strengths of Formula², this task highlights a weakness of the other three languages, in a task that is very common in data-driven applications.
(taskTitle): duration($now - due)
The parentheses are needed because otherwise Formula2 would create an object with a single taskTitle property
(rather than evaluate taskTitle) due to the special handling of the first operand in the colon operator (see Section 4.6.1.2).
Spreadsheets have the same issue as with the previous task: to use a simple formula, we need to perform UI interactions such as dragging down a formula. Otherwise, our only recourse is unwieldy arrayformulas.
But here there is a much bigger issue at play: there is no high-level way to express an interval in a human-readable way.
Spreadsheet applications often provide UI for formatting a number as a duration, but this is not available in formulas and typically produces cryptic separated values of predefined units, so a duration like “2 months, 8 days” may appear like 936:00:00.
Our Lifesheets user study explores this more (see Section 9.7).
Displaying values in any even moderately human-readable way is painful. Even if we only care about differences of a day or more, we need to do low-level wrangling like:
=TRIM(SUBSTITUTE(
IF(DATEDIF(D1, NOW(), "Y") > 0, DATEDIF(D1, NOW(), "Y") & " years, ", "") &
IF(DATEDIF(D1, NOW(), "YM") > 0, DATEDIF(D1, NOW(), "YM") & " months, ", "") &
IF(DATEDIF(D1, NOW(), "MD") > 0, DATEDIF(D1, NOW(), "MD") & " days", ""),
", ", ""))
It gets even worse if we want to show time units as well, as one normally would in a task manager:
=TRIM(SUBSTITUTE(
IF(DATEDIF(D1, NOW(), "Y") > 0, DATEDIF(D1, NOW(), "Y") & " years, ", "") &
IF(DATEDIF(D1, NOW(), "YM") > 0, DATEDIF(D1, NOW(), "YM") & " months, ", "") &
IF(DATEDIF(D1, NOW(), "MD") > 0, DATEDIF(D1, NOW(), "MD") & " days, ", "") &
IF(INT(NOW() - D1) = 0, IF(HOUR(NOW() - D1) > 0, HOUR(NOW() - D1) & " hours, ", "") &
IF(MINUTE(NOW() - D1) > 0, MINUTE(NOW() - D1) & " minutes", ""), "") &
IF(HOUR(NOW() - D1 - INT(NOW() - D1)) > 0, HOUR(NOW() - D1 - INT(NOW() - D1)) & " hours, ", "") &
IF(MINUTE(NOW() - D1 - INT(NOW() - D1)) > 0, MINUTE(NOW() - D1 - INT(NOW() - D1)) & " minutes", ""),
", ", ""))
The ARRAYFORMULA version of this is left as an exercise for the reader.
JavaScript also does not provide a built-in way to format durations in a human-readable way.
In practice, this is often done with a library like moment.js or date-fns,
but for the sake of comparison, we will use a simple, naïve implementation:
task.map(t => {
let start = new Date(task.due);
let end = new Date();
let elapsed = now - start;
let units = [
{ unit: 'year', ms: 365 * 24 * 60 * 60 * 1000 },
{ unit: 'month', ms: 30 * 24 * 60 * 60 * 1000 },
{ unit: 'day', ms: 24 * 60 * 60 * 1000 },
{ unit: 'hour', ms: 60 * 60 * 1000 },
{ unit: 'minute', ms: 60 * 1000 }
];
let rtf = new Intl.RelativeTimeFormat('en', { numeric: 'auto' });
return units.reduce((result, { unit, ms }) => {
const value = Math.floor(elapsed / ms);
if (value !== 0) {
result.push(rtf.format(-value, unit)); // Negative value to represent the past
elapsed -= value * ms;
}
return result;
}, []).join(', ');
});
Standard SQL is not well-suited for this task either, as it is not designed for temporal computations. It is possible to do it, but it is also not pretty:
SELECT taskTitle, CONCAT(
IF(YEAR(due) - YEAR(NOW()) > 0, YEAR(due) - YEAR(NOW()) & " years, ", ""),
IF(MONTH(due) - MONTH(NOW()) > 0, MONTH(due) - MONTH(NOW()) & " months, ", ""),
IF(DAY(due) - DAY(NOW()) > 0, DAY(due) - DAY(NOW()) & " days, ", ""),
IF(HOUR(due) - HOUR(NOW()) > 0, HOUR(due) - HOUR(NOW()) & " hours, ", ""),
IF(MINUTE(due) - MINUTE(NOW()) > 0, MINUTE(due) - MINUTE(NOW()) & " minutes", "")
) FROM task
PostgreSQL however has an age() function that can make this very elegant:
SELECT taskTitle, age(due, NOW()) FROM task
4.7.2Divergent 1-N Relationships: The Decisions App Schema
This is the (Mavo-inferred) schema from the decision-making application that was used in the first lab study (Section 7.1).
It’s a hierarchical schema with two levels of nesting,
where each decision item contains divergent one-to-many relationships.
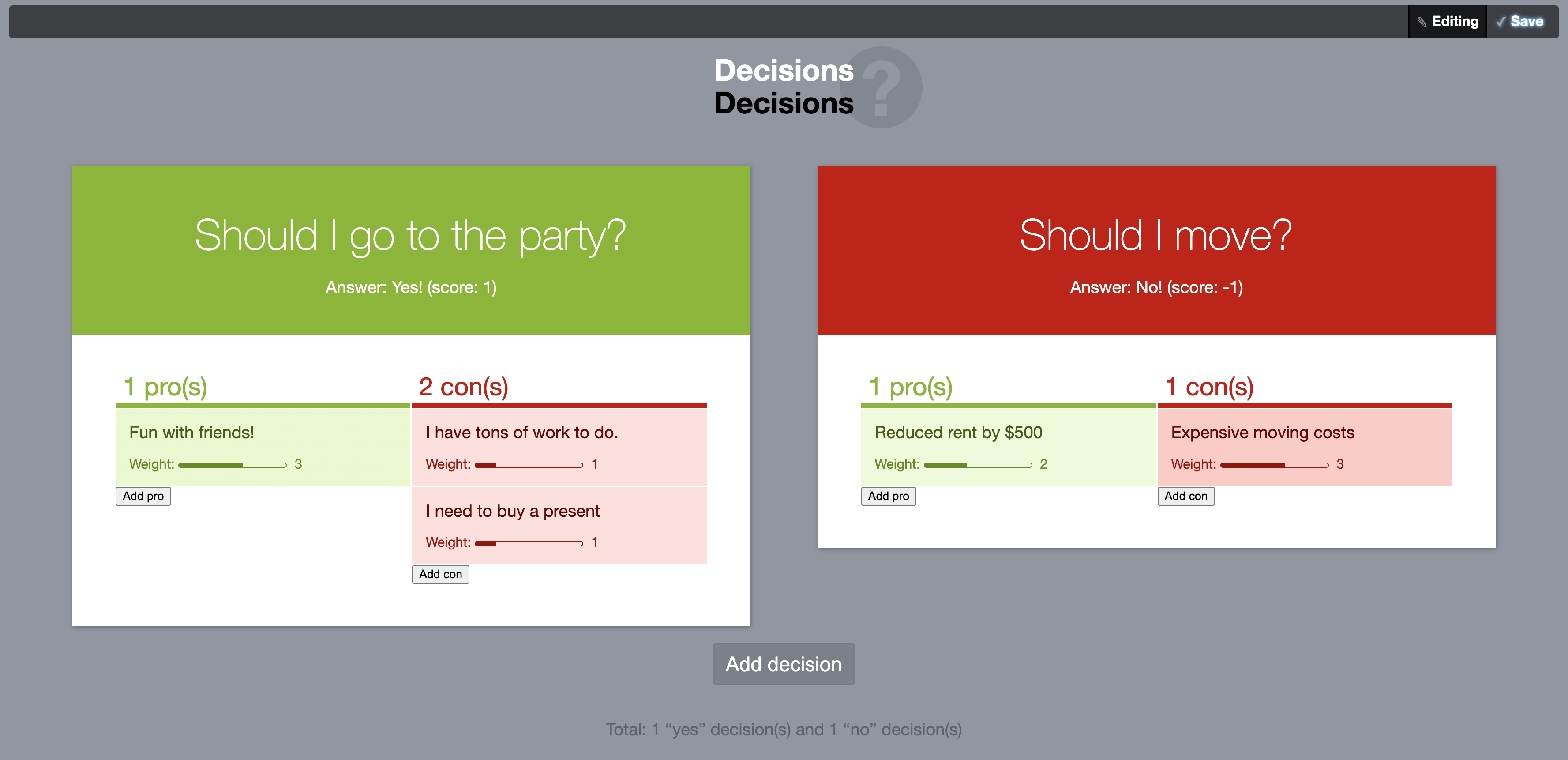
{
decision: [
{
decision: "Should I go to the party?",
answer: null, // calculated
score: null, // calculated
pro: [
{ argument: "Fun with friends!", weight: 3 }
],
con: [
{ argument: "I have tons of work", weight: 1 },
{ argument: "I will need to buy a present", weight: 1 }
]
},
{
decision: "Should I move?",
answer: null, // calculated
score: null, // calculated
pro: [
{ argument: "Reduced rent by $500", weight: 2 }
],
con: [
{ argument: "Expensive moving costs", weight: 3 }
]
}
]
}
| id | decision | score | answer |
|---|---|---|---|
| 1 | Should I go to the party? | ||
| 2 | Should I move? |
| did | argument | weight |
|---|---|---|
| 1 | Fun with friends! | 3 |
| 2 | Reduced rent by $500 | 2 |
| did | argument | weight |
|---|---|---|
| 1 | I have tons of work | 1 |
| 1 | I will need to buy a present | 1 |
| 2 | Expensive moving costs | 3 |
4.7.2.1Calculate the Score of Each Decision
Context node: decision.*
This highlights aggregates that span two separate branches.
sum(pro.weight - con.weight)
or
sum(pro.weight) - sum(con.weight)
SUMIF(pro!A2:A, A2, pro!C2:C) - SUMIF(con!A2:A, A2, con!C2:C)
pro.filter(p => p.decision_id == decision.id)
.reduce((acc, p) => acc + p.weight, 0)
-
con.filter(c => c.decision_id == decision.id)
.reduce((acc, c) => acc + c.weight, 0)
Since SQL does not have a context node concept, we calculate all scores:
SELECT decision.id, sum(pro.weight) - sum(con.weight)
FROM decision
LEFT JOIN pro ON decision.id = pro.did
LEFT JOIN con ON decision.id = con.did
GROUP BY decision.id
4.7.2.2Filtered Aggregate: Count of Good (Score > 0) Decisions
count(score > 0)
COUNTIF(score!A2:A, ">0")
decision.filter(s => s.score > 0).length
SELECT count(*)
FROM decision
WHERE score > 0
4.7.2.3Nested Aggregate: Average Number of Arguments per Decision
This compares nested aggregates across different languages.
average(count(pro) in decision + count(con) in decision)
or
average((count(pro) + count(con)) in decision)
=(SUMPRODUCT((pro!A:A=decision!A2:A3)+0) + SUMPRODUCT((con!A:A=decision!A2:A3)+0)) / COUNTA(decision!A2:A3)
decision.map(d => d.pro.length + d.con.length) / decision.length
SELECT
d.id,
d.decision,
AVG(argument_count) AS average_arguments
FROM
(SELECT
p.did AS id,
COUNT(p.argument) + COUNT(c.argument) AS argument_count
FROM
pro p
LEFT JOIN
con c ON p.did = c.did
GROUP BY
p.did) AS argument_counts
JOIN
decision d ON d.id = argument_counts.id
GROUP BY
d.id, d.decision;
4.7.3Deep Nesting: The Restaurant Reviews Schema
This is the schema from the restaurant review log that was used in the first lab study (Section 7.1). It’s a hierarchical schema with three levels of nesting.
{
"restaurant": [
{
"picture": "https://www.toscanoboston.com/common/images/thumb-cucina.jpg",
"url": "http://www.toscanoboston.com/beacon-hill",
"name": "Toscano",
"visit": [
{
"date": "2016-03-15",
"title": "Date night!",
"dish": [
{
"name": "Filet mignon with black truffle and foie gras",
"dishRating": 4
}
]
}
]
}
]
}
| id | picture | url | name |
|---|---|---|---|
| 1 | “redacted.jpg” | “redacted” | Toscano |
| rid | date | title |
|---|---|---|
| 1 | 2016-03-15 | Date night! |
| vid | name | dishRating |
|---|---|---|
| 1 | Filet mignon with black truffle and foie gras | 4 |
4.7.3.1Nested Aggregate (2 Levels): Restaurant Rating
Context node: restaurant.*
A restaurant’s rating is the average of all visit ratings, and the visit rating is the average of all dish ratings.
average(average(dishRating) in visit)
AVERAGEIFS(
dish!C:C,
dish!A:A,
IF(
ISNUMBER(MATCH(visit!A:A,
IF(restaurant!A:A = A2, visit!A:A, ""),
0
)),
visit!A:A,
""
)
)
visit.map(v => v.dishRating.reduce((acc, c) => acc + c, 0) / v.dishRating.length) / visit.length
SELECT
r.id AS restaurant_id,
r.name AS restaurant_name,
AVG(vr.average_dish_rating) AS restaurant_rating
FROM restaurant r
JOIN visit v ON r.id = v.rid
JOIN
(
SELECT vid, AVG(dishRating) AS average_dish_rating
FROM dish
GROUP BY vid
) vr ON v.rid = vr.vid
GROUP BY
r.id, r.name;
4.7.3.2Filtered Nested Aggregate: Count of Good Restaurants
We define a restaurant as good if its rating is above 3. This is a nested aggregate with three levels of aggregation, and a filter.
count((average(average(dishRating) in visit) in restaurant) > 3)
SUMPRODUCT(
IF(
MMULT(
(visit!A:A = restaurant!A2:A100) *
TRANSPOSE((dish!A:A = visit!A:A) * dish!C:C),
TRANSPOSE((visit!A:A = restaurant!A2:A100) * (visit!A:A <> ""))
) > 3,
1,
0
)
)
restaurant.map(r => r.visit.map(v => v.dishRating.reduce((acc, c) => acc + c, 0) / v.dishRating.length) / r.visit.length).filter(r => r > 3).length
WITH restaurant_ratings AS (
SELECT
r.id AS restaurant_id,
AVG(vr.average_dish_rating) AS restaurant_rating
FROM restaurant r
JOIN visit v ON r.id = v.rid
JOIN (
SELECT
vid,
AVG(dishRating) AS average_dish_rating
FROM dish
GROUP BY vid
) vr ON v.id = vr.vid
GROUP BY r.id
)
SELECT COUNT(*) AS good_restaurant_count
FROM restaurant_ratings
WHERE restaurant_rating > 3;
4.8Discussion & Future Work
4.8.1Limitations
Formula2 was designed to make the kinds of computations that are common in small-scale data-driven applications easier to express by novices. There are numerous use cases arising in general application development that are currently either awkward or impossible to express in Formula2.
4.8.1.1Complex Mapping Operations
While Formula2 can express simple mapping operations very easily, such as mapping objects to a descendant property or a combination of descendant properties, many of the kinds of arbitrary mapping operations that a developer can accomplish in an imperative language via a loop are not possible, or awkward to express with Formula2 alone.
A large class of such use cases is augmenting objects, such as the triangle hypotenuse example in Section 4.5.5.3, which can be expressed but the formula to express them is beyond the capabilities of most novices.
4.8.1.2String Parsing
One big category is parsing tasks: producing structured data from a string of text, for example color components from a serialized color, or SVG path segment information from an SVG path string (see Section 8.2.1).
Perhaps a novice-friendly way to express simple patterns could be developed and exposed in Formula2 via suitable functions, but currently this remains an open question.
4.8.2Is Flattening Always the Right Choice?
Possibly one of the most questionable design decisions of Formula2 is its flattening of multi-dimensional arrays.
E.g. list(1, list(2, 3), list(4, 5)) is flattened to list(1, 2, 3, 4, 5).
The intent behind this was to simplify the number of distinct cases that need to be handled,
since these structures did not naturally occur in Mavo apps,
and since every multi-dimensional array can be expressed as an array of objects.
However, since the original design, some cases have emerged where this flattening is undesirable.
The main example is grouping by nested lists.
Consider a list of people (person), each of whom has a list of hobbies (just a list of strings) (hobby).
Currently, person by hobby would not produce a reasonable result, since it depends on element-wise matching.
Perhaps a compromise solution could be to use a data structure that behaves like a flattened array, but is not actually flattened. Or the opposite: a flattened array that preserves metadata about the boundaries of its constituent arrays.
4.8.3Dot Notation for Function Calls
We opted for a functional syntax, as it appears to be easier for novices to understand,
and may be familiar from spreadsheets.
We hypothesized that for example, count(rating) is easier to understand than rating.count().
However, it does come with the drawback of authors having to manage nested parentheses,
a common authoring mistake.
Additionally, if some functions are available as functions and some as methods,
it increases the cognitive load on the author to remember which is which.
In line with our design principle of robustness, it appears an optional dot notation could greatly increase the efficiency and safety of Formula², without compromising its learnability.
Rather than authors having to remember which functions are methods,
every function would be available as a method and vice versa.
arg.foo(arg1, arg2) would be equivalent to foo(arg, arg1, arg2).
This would allow authors to use the syntax that is most convenient for their use case, and feels most natural to them, without introducing additional error conditions or cognitive tax.
4.8.4Notation for Unrestricted Identifiers
We have repeatedly seen in our user studies that novices struggle with the concept of identifiers having a restricted syntax. Furthermore, imposing restrictions on identifier names makes it awkward to work with data created by others, which may not conform to these restrictions.
To prevent syntactic ambiguity, allowing unrestricted identifiers would require a different syntax to tell the parser that a series of symbols is actually an identifier, and delineate where it begins and ends.
It appears that brackets ([]) could be a good fit for this purpose, and have some precedent ([10]).
However, this would require substantial changes in Mavo, which uses brackets to embed Formula² expressions in literal text.
4.8.5Quantities as a First-class Citizen
For functions returning a numerical value with no arguments, and constants, it is often more readable to be able to express multiplications with a fixed number as a number with a unit.
For example, date($today + 2 * days()) will return the date two days from now.
But it might be a lot more natural if we could write date($today + 2days).
Or, rather than calculating a circle’s circumference as radius * 2 * pi,
it may be more readable to write radius * 2pi.
Formula² could implement this as a general language construct: a number followed by an identifier is syntactic sugar for the multiplication of the number and the value of the identifier if the identifier is a number, or the value of calling the identifier as a function with no arguments if the identifier is a function. This could be a property of specific functions, since it only makes sense for a relatively small percentage of functions. Alternatively, the number and type of quantity could be retained in an object that can be coearced to a number when needed. This could allow expressing a lot more values as first-class citizens, e.g. currencies, temperatures, measurements, etc.
4.8.6Optimizing Frequent Lookups
While performance optimizations do not affect the language itself, in practice they can have a significant impact on the user experience. Currently, the only performance optimization that the prototype implementation of Formula2 employs is the use of a schema to precompute all possible property paths. Even caching the result of an expression so that expressions are not re-evaluated if the data has not changed, is relegated to the host environment.
However, given the lack of abstractions in the formulas novices write (see [25] and Section 9.8),
more elaborate caching mechanisms are essential.
By moving caching within Formula2, individual operands can be independently cached,
so that for example task by priority and count(task by priority) only needs to compute the grouping once.
Additionally, a common pattern we have observed (see Chapter 7) is for certain properties to be repeatedly used to filter the same structure, often acting essentially as implicit primary keys.
For an illustrative example,
consider a collection of books and their metadata (possibly fetched from a remote API),
and a reading log with a list of books read, ratings, and notes, maintained by the app user.
The app author could display a dropdown of books to associate each entry with,
and store the selected book ID in a bookId property.
Then, to display book metadata next to each entry, the author would have to run a filtering operation such as
books where id = bookId.
The problem with that is that this would iterate over the entire books collection for each entry,
making lookups O(N2).
These types of tasks are the bread and butter of relational database systems: you simply declare bookId as a foreign key,
and assuming book.id is a primary key, the database will take care of the rest.
However, this is nontrivial for novices and end-user programmers, who struggle to think in terms of relations [26]
and are goal-oriented, and therefore averse to preparatory work such as setting up schemas and indices.
However, perhaps end-users don’t need to do this work.
Assuming Formula2 provided a mechanism for declaring primary keys and indices,
creating them could be handled by the host environment,
which has a lot more information about what expressions may be evaluated and how frequently.
To use Mavo as an example, a simple heuristic would be to automatically create indices for any property used in a where or by clause
within a collection.
Another (not mutually exclusive) direction could be for Formula2 to automatically optimize expressions based on a combination of factors such as how frequently they are evaluated, and how large the collections they operate on are.
4.8.7Short-circuit Evaluation
Most common programming languages support short-circuit evaluation for logical and conditional(ternary) operators.
Later operands are only evaluated if earlier operands do not suffice to determine the value of the expression.
For example, in a and b, if a is false, b is not evaluated, since we already know that the overall value must be false.
Due to its handling of list-valued operations, Formula² cannot support short-circuit evaluation, as all operands need to be examined to determine the shape of the result.
This is not an issue for its use as a reactive formula language, but becomes one once side effects are introduced (such as by Data Update Actions, see Section 6.3.4).
4.9Conclusion
In this chapter, we presented Formula2, a formula language designed for end-user programming in data-driven web applications, and optimized for hierarchical schemas.
Our user studies (described in Chapter 7) have shown that Formula2 is easy to learn for novices, who often did not believe that expressions they wrote could work.
While Mavo is currently the only deployed Formula2 host environment, we believe its potential is much broader, and look forward to seeing additional implementations in the wild.
This is a simplification and would result in very poor performance. In practice, the Breadth-First Search is performed on a precomputed schema of the data, and then the paths are resolved on the actual data. ↩︎
The implementation of Formula² that the Mavo HTML prototype embeds does not actually follow this; a bug that has caused a lot of confusion. ↩︎
The only exception is years, since something like
"1997"is actually a valid ISO date. However, this does not participate in the heuristic discussed here, since if authors are doing math between years, there is nothing special to do — handling them as regular numbers works fine. ↩︎JSEP: ericsmekens.github.io/jsep ↩︎
The productions do not enforce operator precedence, which is specified seprately, and do not describe the minutiae of number and string literals, which are on par with JavaScript or similar languages. ↩︎